¿Qué Es ECDSA? ¿Cómo Funciona En Bitcoin?

ECDSA es la abreviación de Algoritmo de Firma Digital de Curvas Elípticas (por sus siglas en inglés). Se trata de un esquema de criptografía basado en curvas elípticas, también conocidas como Curvas Elípticas Criptográficas o ECC (por sus siglas en inglés).

El algoritmo ECDSA utilizan las curvas elípticas y los campos finitos en función de firmar la información para que un tercero luego pueda verificar la autenticidad de la misma. Todo mientras el firmante mantiene la exclusividad de poder ser el creador de la firma.

En el caso de Bitcoin, esta firma se utiliza para firmar el traspaso de la propiedad de los BTC al demostrar que es el único que puede crear esa firma.

ECC

Pero antes de que veamos en detalle todo esto de ECDSA, es necesario entender un poco que es todo esto de curvas elípticas.

¿Quién creo ECC y cuando?

El concepto de criptografía basada en curvas elípticas fue propuesto de manera independiente por los matemáticos Neil Koblitz y Victor S. Miller en el año 1985.

Sin embargo, no fue hasta principios de 2000 que este concepto fue utilizado por la criptografía en cuestiones prácticas, cuando los proveedores de internet le encontraro un uso.

¿Cómo se usa ECC en las criptomonedas?

La criptografía, que es la base de los esquemas de firma digital de las criptomonedas, permite verificar de forma descentralizada las transacciones entre dos partes.

Anteriormente, se utilizaba un método de encriptación denominado RSA, pero ECC tiene grandes ventajas sobre este.

Para empezar las claves utilizadas por ECC son mucho más pequeñas en tamaño que las de RSA. Y todo mientras provee del mismo nivel de seguridad.

Por otro lado, aunque la encriptación RSA es ampliamente utilizada en internet, ECC es más eficiente, por lo que fue la elegida para ser usada en las criptomonedas, en especial por Bitcoin.

¿Quién creo ECDSA y cuando?

El concepto de ECDSA fue introducido mucho después de ECC, concretamente en 1992. Su creador, un matemático y criptógrafo canadiense, es Scott Vanstone.

¿Cuál es el objetivo de ECDSA en Bitcoin?

Sabemos que la tecnología que facilita Bitcoin hace una reinterpretación del concepto de derecho de propiedad.

Cuando hablamos de este en un sentido más tradicional, el de ser dueños de una casa, una suma de dinero, etc., nos referimos a almacenar físicamente y legalmente este objeto en persona, o transferirlo a una estructura de confianza, como puede ser un banco, para que lo haga por nosotros.

En el caso de Bitcoin, todo es diferente. Los BTC no son almacenados en un lugar centralizado o localmente, no hay ninguna estructura que actúa como su custodio.

Los bitcoins existen complementé en la cadena de bloques, en copias que están distribuidas por toda la red y que se almacenan en ordenados llamados nodos que están conectados entre sí.

Por tanto, ser dueño de bitcoins significa que tenemos la habilidad para transferir el control de los mismos a otro usuario mediante la creación de un registro en la cadena de bloques, una transacción.

Y esto es posible gracias a ECDSA y el par de claves, la clave pública y la clave privada.

ECDSA se compone de dos procedimientos separados, uno para la firma y otro para la verificación. Siendo que cada procedimiento consiste en un algoritmo compuesto por varias operaciones aritméticas.

En el algoritmo de firma utilizamos la clave privada, mientras que en el algoritmo de verificación hacemos uso de la pública.

¿Qué es una curva elíptica?

Una curva elíptica en álgebra es representada con una ecuación que tiene el siguiente formato:

y² = x³ + ax + b

Siendo a = 0 y b = 7 (en la versión utilizada por Bitcoin), y tiene una forma que se ve de esta manera:

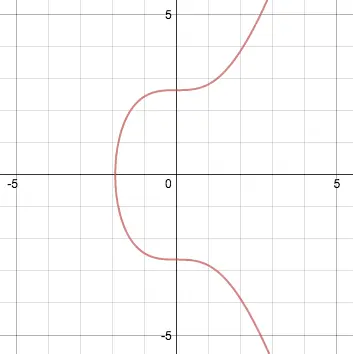
Las curvas elípticas son útiles porque poseen varias propiedades.

En primer lugar, las curvas elípticas son grupos. Los grupos están definidos en las matemáticas si tienen:

1. Cierre: si a y b se encuentra en el grupo G, entonces a + b también se encuentra en el grupo G
2. Asociatividad: (a + b) + c = a + (b + c)
3. Elemento de identidad: a + 0 = 0 + a = a
4. Por cada a existe un b tal que a + b = 0
5. Solo para grupos abelianos, conmutatividad: a + b = b + a

Por otro lado, las curvas elípticas tienen sus propias leyes de grupo específicas:

1. El elemento identidad es el punto en infinito, 0
2. El inverso del punto P es el simétrico respecto al eje x
3. La adición se define como: dados tres puntos alineados y distintos de cero, P, Q y R se tiene P + Q + R = 0. El orden no importa para estos tres puntos, por lo que P + (Q+R) = 0, (P+Q) + R = 0, (P+R) + Q = 0, etc. Esto nos permite demostrar que las curvas elípticas son conmutativas y asociativas.

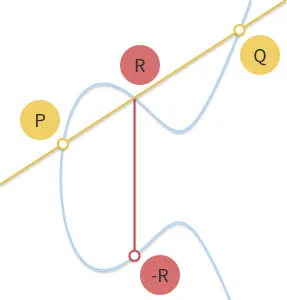
La ecuación anterior también nos da una ecuación para sumar dos puntos y calcular el tercer punto. Como ya hemos dicho, sabemos que cuando una recta pasa por dos puntos de una curva, pasará por un tercer punto. Y sabemos que:

P + Q + R = 0

Entonces

P + Q = R

Y sabemos que -R es la inversa del punto R reflejado en el eje x.

En el caso de que P es tangente a la curva, entonces solo existen 2 puntos de intercepción.

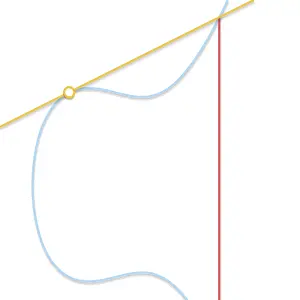
Ya que P es tangencial a la curva, entonces tenemos que P = Q y, por tanto, P + P = -R, obtenido de la ecuación de arriba. O lo que es agua a 2P = -R. Esto se conoce como duplicación de puntos para las curvas elípticas.

¿Qué son los campos finitos?

Los campos finitos, como su nombre lo indica, es un grupo de números finitos. Los números reales son un grupo de números infinitos, pero un grupo compuesto por (3, 96, 235, 1.891, 15) es un grupo finito.

Un conjunto de números más interesante y útil es el conjunto de enteros módulo p, donde p es un número primo. El módulo es como la suma en un reloj o la matemática del resto.

Por ejemplo, el módulo 12 sería como sumar alrededor de un reloj, así que 1 + 4 en módulo 12 = 5, pero 1+15 en módulo 12 = 4. La razón de esto la encontramos en un reloj. 1 + 15 = 16 y 16 es 4 horas después de 12. O podemos verlo de forma matemática con los restos. 16 / 12 = 1 y su resto es 4.

¿Cómo se combinan los campos finitos con las curvas?

Cuando combinamos los campos finitos y las curvas elípticas obtenemos la magia de la criptografía. Así la ecuación de la curva elíptica se transforma de la siguiente forma:

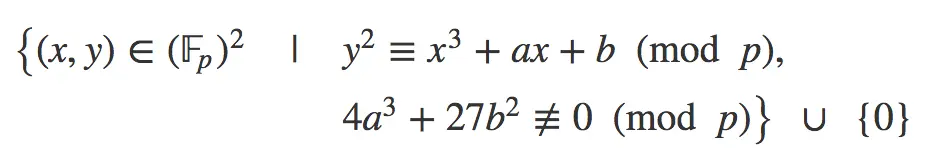
Básicamente, agregamos módulo de P al final de la ecuación que habíamos visto antes.

Y si dibujamos un campo finito sobre una curva elíptica, obteneos los siguientes ejemplos:

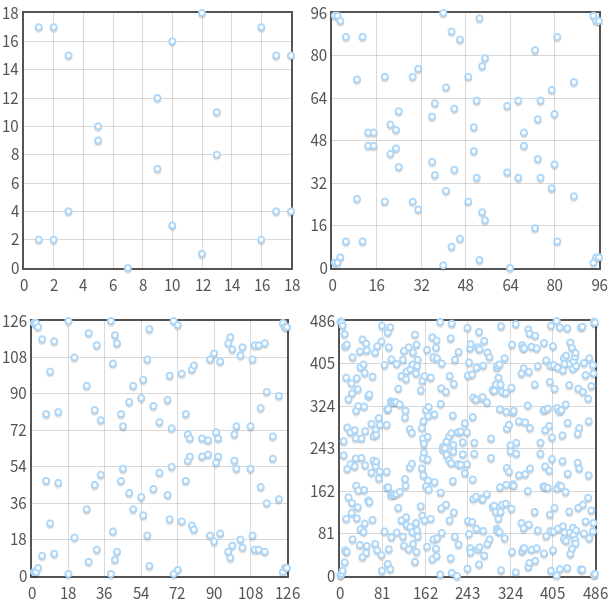
Aquí podemos observar que los puntos son simétricos de acuerdo a cierta línea, lo que significa que todavía podemos realizar la suma de puntos P + Q = -R, donde dibujamos una línea conectando P, Q y R y reflejamos R sobre el eje x para hallar -R.

En un campo finito, una línea se ve muy diferente a la que encontramos en un campo infinito. Es como esos videojuegos en donde atravesamos la parte superior de la pantalla para volver a la parte de abajo.

Esto se debe a que cuando el número sobrepasa al módulo del campo finito este retorna y continua al valor del resto del módulo.

Aquí debajo hay un gráfico donde P, Q y R son conectados a través de una línea.

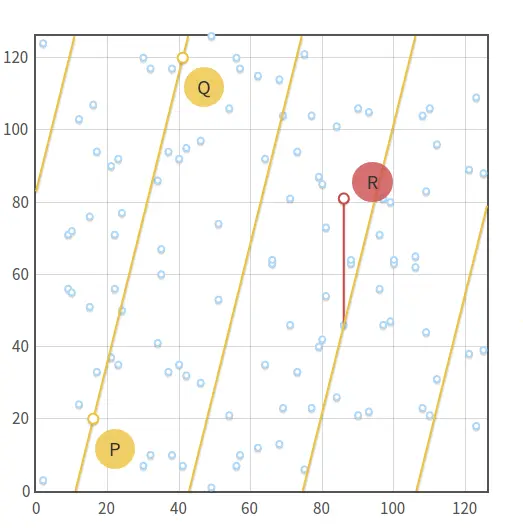
Y como los campos finitos sobre la curva elíptica siguen siendo un grupo, mantenemos todas las propiedades de un grupo matemático que vimos antes.

Multiplicación Escalar y Orden

Si recordamos lo que hablamos antes, sabemos que una linea que pasa por dos puntos en una curva elíptica también pasara por un terceroo y la ecuación para calcular ese punto es P + Q = -R (adición de puntos).

Además, si P es tangencial a la curva elíptica entonces P = Q y P + P = -R o 2P = -R (duplicación de puntos).

La adición de punto y la duplicación de punto nos permite definir la multiplicación escalar para la curva eliptica de forma que xP = R donde x es un escapar, P es un punto tangente de la curva y R es el punto resultante de sumar P sobre sí mismo x veces. Por ejemplo:

• 11P = R
• P + 10P = R
• P + 2(5P) = R
• P + 2(P + 4P) = R
• P + 2(P + 2(2P)) = R

En este ejemplo, tomamos el punto P y sumamos el punto P para obtener el nuevo punto F.

P + 2(P + (2F)) = R

Tomamos el punto F y le añadimos F para obtener el nuevo punto C.

P + 2(P + C) = R

Suma P y C para obtener el punto D.

P + 2(D) = R

Suma el punto D al punto D para obtener el punto E.

P + E = R

Así sumamos el punto P y el punto E para obtener R. De esta forma vemos cómo la adición de puntos y la duplicación de puntos nos permite calcular la multiplicación escalar para xP = R.

Las curvas elípticas sobre campos finitos tienen la misma propiedad. Podemos sumar continuamente P sobre sí misma creando una multiplicación escalar.

Volviendo al ejemplo del reloj que utilizamos para las operaciones de módulo. Al añadir P a sí mismo una y otra vez, es similar a mover P alrededor de un reloj. Al final, volveremos al punto de partida y pasaremos continuamente por los mismos puntos.

Vemos un ejemplo usando la ecuación:

y² = x³ + ax + b (mod 97)

Si elegimos el punto P = (3, 6) podemos girar a t’raves de la multiplicación escalar de P para entender cuantas veces agregamos P a sí mismo para volver al punto (3, 6).

Podemos ver que para P = (3,6) se necesitan 5P para volver al mismo punto (3,6). Eso significa que funciona P = (3,6) y también 6P, 11P, 16P, etc.

El punto interesant a entender del ejemplo anterior es calcular el orden de un subgrupo generado por el punto P. El orden de P se define como el menor número entero positivo n tal que nP = 0. Así que en nuestro ejemplo, el orden del subgrupo basado en el punto P es 5, lo que significa que 5P = 0. No hay ningún multiplicador escalar positivo más pequeño del punto P que dé lugar al punto 0.

Uniendo todo esto, nuestro ejemplo define lo siguiente:

• Módulo primo del campo finito = 97
• La curva elíptica descrita anteriormente donde a = 2 y b = 3
• Un punto aleatorio P = (3,6), llamado punto base
• El orden del subgrupo (conjunto de puntos cíclicos basados en P) = 5

¿Cómo funciona ECDSA en Bitcoin?

Para Bitcoin tenemos los siguientes parámetros:

• Módulo primo: 2²⁵⁶ – 2³² – 2⁹ – 2⁸ – 2⁷ – 2⁶ – 2⁴ – 1 → es un número realmente muy grande que equivale aproximadamente a todos los átomos del universo. También se representa en hexadecimal como: FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F
• Curva elíptica donde a = 0 y b = 7
• Punto base P en hexadecimal: 04 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8
• Orden en hexadecimal: FFFFFFFF FFFFFFFF FFFFFFFF BAAEDCE6 AF48A03B BFD25E8C D0364141

Estos números no se eligieron de forma aleatoria. Estos son actualmente un estándar criptográfico propuesto por la organización Standars for Efficiente Cryptography Group (SEC), y Bitcoin utiliza el estándar secp256k1.

Por tanto, la clave privada de Bitcoin es solamente un número aleatorio elegido entre 1 y el orden de arriba. A partir de esta se puede derivar la clave pública, todo gracias la siguiente fórmula:

clave pública = clave privada * punto base

Esto es simplemente realizar una multiplicación escalar en el punto base P multiplicado por su clave privada de la misma manera que describimos la multiplicación escalar arriba con xP = R.

En el ejemplo anterior mostramos cómo x = 11 y calculamos 11P = R usando la duplicación de puntos y la adición de puntos.

La diferencia entre este ejemplo y Bitcoin es que Bitcoin utiliza números extremadamente grandes en forma hexadecimal, pero el proceso de usar la duplicación de puntos y la suma de puntos es el mismo.

Una vez que seleccionamos la clave privada y la multiplicas por el punto base P, obtenemos un nuevo punto (x, y) en el campo finito/curva elíptica. Esa es nuestra clave pública.

Es computacionalmente fácil usar la clave privada y multiplicarla por el punto base para obtener la clave pública, pero es computacionalmente difícil empezar con la clave pública y trabajar hacia atrás para calcular la clave privada. La ecuación es un camino de ida.

Desventajas de ECDSA

Con ECDSA, el actual método para firmar transacciones de Bitcoin, no tiene soporte de forma nativa a la multi firma, por lo que debe ser implementado usando una especie de contratos inteligentes llamados Pay-to-Script-Hash (P2SH).

Este número aparentemente aleatorio determina la propiedad de las monedas. En el momento del gasto, el titular abre el script y la clave para descifrar el hash al mismo tiempo.

Entonces, cada usuario puede utilizar el hash original para verificar la veracidad del script y cumplir las condiciones de la transacción.

Sin embargo, al mismo tiempo, los usuarios deben revelar todas las condiciones de la transacción, incluidas las que no se han cumplido. Por ejemplo, las monedas pueden gastarse si nosotros y nuestro amigo firmamos la transacción, o solo nuestro amigo la firma al final de la semana, o solo nosotros lo hacemos.

El primer problema de este modelo es la falta de privacidad. Para las transacciones P2SH, es necesario que las direcciones comiencen con el número 3. Esto da a los analistas de la cadena la oportunidad de reconocer todas las transacciones P2SH en la red y determinar las direcciones implicadas en multi firma.

El segundo problema es la gran cantidad de datos que hay que procesar, ya que P2SH requiere conocer las claves públicas de todos los participantes en la multi firma.

El esquema de firma Schnorr y la tecnología Taproot resuelven estos problemas.